Programación Gráfica 2D ( VI )
|
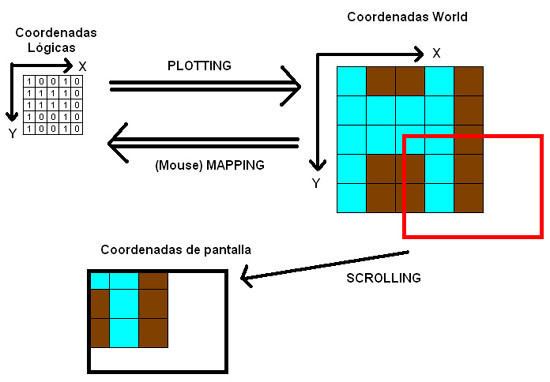
IntroducciónEn el último tutorial explicaba como dibujar mapas isométricos, y como realizar el proceso de “plotting”. El proceso inverso, de convertir las coordenadas de pantalla a coordenadas lógicas (mapping), lo dejaba aparcado porque era bastante más complicado. Pues bueno, ha llegado el momento de explicarlo:
RecordatorioAntes de nada, vamos a ver en qué consistía el “mouse mapping” en los mapas 2D clásicos:
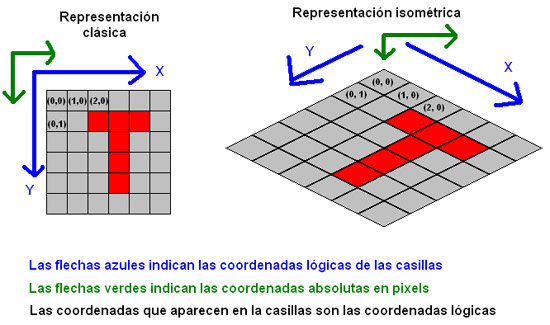
Simplemente, se trataba de coger unas coordenadas de pantalla, en pixeles, y obtener las coordenadas lógicas de la casilla que ocupa ese lugar. Esto era muy útil, por ejemplo, para averiguar sobre qué casilla está el ratón, o para realizar optimizaciones más adelante. Con los mapas rectangulares, esto era muy fácil, bastaba con hacer una división. Como los tiles eran rectangulares también, no había problemas. Sin embargo, ahora eso no es tan simple. Los tiles tienen forma de rombo, y los ejes de coordenadas lógicas y absolutas son completamente distintos:
Asi que hacer el mapping va a ser más difícil. Empezaré explicando el método tradicional que se suele usar, basado en una imagen de referencia. Este método funciona con cualquier tipo de mapa y cualquier relación de ancho / alto. Después comentaré un segundo método, más sencillo pero también más limitado.
La rejillaHemos dicho que calcular coordenadas en mapas rectangulares es muy fácil. ¿Por qué no probamos a “transformar” el problema en algo así?. Podemos dividir el mapa en una “rejilla” rectangular, que es bastante sencilla de calcular:
Cada rectángulo de la rejilla tiene exactamente el tamaño de un tile, y el rectángulo (0, 0) está alineado con la casilla (0, 0). Hay que recordar que la casilla (0, 0) también hace de centro de origen de las coordenadas absolutas. Con esto, averiguar las coordenadas del rectángulo (coordenadas de rejilla) en el que está el cursor es tan fácil como lo era en los mapas rectangulares. Simplemente basta con dividir. rejilla.x = mouse.x / TILE_ANCHO;
NOTA: Antes de esto, hay que ajustar mouse para tener en cuenta el scroll. Basta con sumar el desplazamiento a las coordenadas de pantalla.
La imagen de referenciaBien, ahora que sabemos qué rectángulo de la rejilla contiene a la casilla pulsada, vamos a echar un vistazo más de cerca a ese rectángulo:
Vemos que hay 5 casillas en el rectángulo que han podido ser pulsadas. La del centro en gris, y las 4 “vecinas”, cada una marcada en un color. ¿Como saber cual de todas es la que ha sido pulsada? Bueno, en primer lugar, podemos averiguar cual es la posición del cursor DENTRO del rectángulo (es decir, el pixel exacto del rectángulo que se pulsó), esto es tan simple como hacer un módulo: indice.x = mouse.x % TILE_ANCHO; En el caso de estar usando coordenadas negativas, indice.x (o indice.y) serán negativos, lo que significa que nos estamos saliendo del rectángulo de la rejilla. En ese caso, nos “desplazamos” al nuevo rectángulo en el que está el índice, y ajustamos los nuevos valores: if (indice.x < 0) {
indice.x += TILE_ANCHO;
--rejilla.x;
}
Y lo mismo para indice.y
Y ahora, conociendo el pixel, ¿por qué no mirar el color en la imagen que he puesto antes?. Si el color en ese pixel es verde, entonces sabemos que la casilla pulsada es la de arriba a la derecha. Usaremos una imagen de referencia exactamente igual que la que he puesto antes, donde cada casilla viene en un color distinto. Mirando el color del pixel pulsado, podemos saber a qué casilla pertenece: switch (imagenReferencia[indixe.x][indice.y].colorPixel) {
case gris:
casilla = CENTRO;
break;
case azul claro:
casilla = NO;
break;
case verde:
casilla = NE;
break;
case azul oscuro:
casilla = SO;
break;
case amarillo:
casilla = SE;
break;
}
Nota: En realidad, usaremos un array bidimensional con las dimensiones del tile, pero con números en lugar de colores. Por ejemplo, el número 3 significaría la casilla al SO, o el 4 la del SE. Esto es mejor porque acceder a un array es más rápido que bloquear una superficie, leer un pixel, y descodificar el color.
WalkingCon todo esto ya tenemos lo suficiente para saber qué casilla fue pulsada. ¿Pero como calculamos sus coordenadas? Para eso usaremos el “tileWalker” que se vió en el otro tutorial. Básicamente, el proceso completo es:
Las coordenadas resultantes son las de la casilla pulsada. ¿Pero como calcular las coordenadas de la casilla centro del rectángulo? Echemos un vistazo a la imagen anterior:
Vemos que, gracias a que los recuadros se alinean con la casilla (0, 0), podemos ir “caminando” con el tileWalker a cualquiera de ellos. Por ejemplo, para ir al rectángulo (1, 2), desde la casilla (0, 0), podemos movernos un paso al Este, y dos al Sur. Para ir al rectángulo (3, 2), nos movemos 3 al Este, y 2 al Sur. Para ir al rectángulo (x, y), nos movemos x al Este, y y al Sur. casilla = tileWalk (ISOD_E, Punto(0,0), rejilla.x); Nota: También funciona con valores negativos. Y después simplemente daremos el último paso que nos indique la tabla de referencia dependiendo del color. Y el resultado serán las coordenadas lógicas de la casilla pulsada, que será el valor que devuelva la función. ¿Facil, verdad? xD
Otro métodoComo he comentado antes, este método de la imagen de referencia funciona con cualquier mapa y cualquier relación de aspecto. Pero si sabemos que siempre vamos a usar mapas con forma de rombo, y que la relación siempre va a ser 2:1, podemos simplificarnos bastante la vida, usando el siguiente código: x0 = mouse.x – (TILE_ANCHO/2); y0 = mouse.y; casilla.x = y0 + (x0 / 2); casilla.y = y0 – (x0 / 2); casilla.x /= TILE_ALTO; casilla.y /= TILE_ALTO; Para saber de donde sale esto os recomiendo mirar este tutorial. Nosotros usamos como valor de ajuste horizontal en x0 la mitad del ancho del tile, dado que nuestro origen de coordenadas no está en el centro de la casilla, sino en la esquina superior izquierda del rectángulo del tile. Comentaré mas sobre anclas y desplazamientos en futuros tutoriales.
OptimizacionesHay que recordar que estamos dibujando el mapa COMPLETO en cada fotograma. Esto simplemente es inaceptable. En cuanto el mapa sea un poco grande, irá lentísimo. Lo que nos interesa es hacer como hacíamos con los mapas rectangulares, y dibujar solamente el “trozo” del mapa que está en la pantalla. Pero para eso hay que cambiar el orden de dibujado:
A partir de ahora usaremos el orden “izquierda->derecha, arriba->abajo”. El algoritmo de dibujado se puede dividir en varias fases:
Bueno, pues empecemos.Esto lo voy a explicar rapidito xD
Fase 1Para calcular las casillas sobre las que están cada esquina, usaremos el mismo proceso de “mouse mapping” que hemos usado antes (el primero). Sólo que con una variación. Nos detendremos cuando hayamos calculado las coordenadas de la casilla “centro” del rectángulo. No nos interesa calcular la casilla exacta.
La razón de eso es porque las casillas “centro” siempre están alineadas. Mientras que con las casillas exactas no ocurre eso. Fijaros en la imagen como las casillas amarillas de abajo no están en la misma columna que las superiores. Para que el algoritmo funcione, necesitamos que las casillas “límite” estén siempre alineadas.
Fase 2Al usar únicamente las casillas centro, pueden darse situaciones como esta:
En este caso, las casillas verdes nunca se dibujarían, aunque parte de ellas caen dentro de la pantalla. Por lo tanto, tenemos un problema. La solución es simple, basta con ampliar el marco de dibujado, alejándonos de los bordes de la pantalla un paso: supIzq = tileWalk (ISOD_NO, supIzq, 1); supDch = tileWalk (ISOD_NE, supDch, 1); infIzq = tileWalk (ISOD_SO, infIzq, 1); infDch = tileWalk (ISOD_SE, infDch, 1); NOTA: En el caso de dibujar objetos, tendremos que desplazar los limites inferiores hacia abajo, para asegurarnos de que aunque la casilla en la que está el objeto caiga fuera de la pantalla, la parte superior del mismo se dibuje correctamente. Si la altura máxima de los posibles objetos es h, desplazaremos hacia abajo (h / TILE_ALTO) veces.
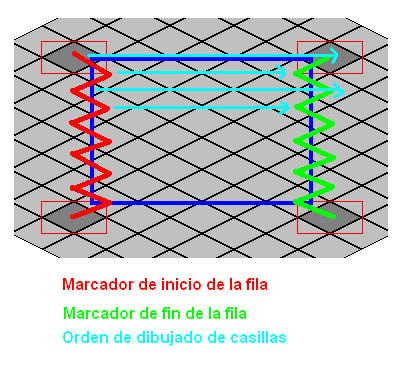
Fase 3Una vez hemos hecho todo lo anterior, la tercera fase es bastante simple. Tendremos dos marcadores que nos indicaran la casilla inicial y final de cada fila de casillas. Iremos moviendo esos marcadores hacia abajo, y por cada fila, dibujamos todas las casillas de izquierda a derecha.
Un par de cosas a tener en cuenta es que los marcadores no los movemos al sur, porque nos saltaríamos filas, sino que los movemos alternativamente al SO, y SE. Y cuando un marcador se mueve en una dirección, el otro lo hace en la contraria. Es decir, si el marcador de inicio se mueve al SO, el de fin lo hace al SE, y viceversa. Teneis los detalles implementados en el siguiente código: void MotorGrafico::dibujar (Rectangulo area) {
//Coordenadas de las esquinas
NOTA: Como veis en el código, no dibujamos la pantalla, sino un rectángulo llamado “area”. Por lo general, area abarcará toda la pantalla, asi que dará igual. Pero al hacer esto tenemos la opción de dibujar regiones más pequeñas si nos hace falta mas adelante.
Y esto es todo, un saludo.
|