Introducción
Con el último tutorial ya terminé de explicar el funcionamiento de SDL y la programación gráfica en 2D (bueno, relativamente, pero se supone algo de investigación por parte de cada uno).
Así que a partir de ahora voy a empezar a hablar sobre técnicas reales para programar juegos. Hay cientos, y podría ponerme a hablar tanto de los Sprites, animaciones, etc... como de sistemas de optimización.
Pero creo que viendo nuestro proyecto, lo más util es que comente un poco en qué consiste el tilemapping. Algunas palabras como “tiles” (casillas en español), o “tileset” ya están apareciendo bastante, así que voy a ver si consigo explicarlo un poco mejor.
Voy a hablar sólamente sobre el tilemapping completamente en 2D (es decir, visto desde arriba). Nada de isométrico de momento. Cuando ya esto quede claro, en el siguiente tutorial empezaremos con los motores isométricos.
Por cierto, para los que no sois de la parte gráfica, os recomiendo que lo leais de todos modos. Este tutorial y los siguientes son los que van a explicar QUE es un mapa, QUE tiene que guardar una casilla, y POR QUE, QUE coño es un tileset, etc...
Asi que puede que os interese. Además, no voy a meterme para nada en cosas de SDL como formatos de pixels o cosas así. Es bastante más light en ese sentido.
Vamos, no hace falta que os lo aprendais de memoria (eso solo los de gráficos xD), pero si que tengais una idea cuando os toque programar la clase "Casilla" de que es lo que se le va a pedir y por qué.
¿Qué es el tilemapping?
Bueno, asi a lo simple el tilemapping es dividir el terreno (o mapa) de juego en casillas iguales, a las que se les llama “tiles”. Cada una de estas casillas puede tener un gráfico distinto, y juntando muchas casillas se consigue un mapa complejo de una manera sencilla.
Un ejemplo: Hundir la Flota
En este juego, el mapa es una cuadrícula de casillas. Cada casilla puede tener varios estados (agua, barco, barco tocado, barco hundido, etc...). Y cada uno de estos estados se representan en pantalla cambiando el color de la casilla, o usando una imagen distinta.
A la hora de dibujar la cuadrícula usando una librería de programación gráfica 2D como SDL lo que haremos será recorrer todo el mapa, y dibujar el gráfico (o tile) que corresponda dependiendo del estado, en la posición que sea.
Algunas imágenes de juegos con tilemapping:
http://www.blitz.sos-software.co.uk/assets/scrs/full/tilemap.jpg
http://www.blitz.sos-software.co.uk/assets/scrs/full/bmax_tilemap.jpg
http://www.tilemap.co.uk/images/aescr020.gif
Representación
Lo que nos permite este sistema es representar el mundo del juego de una forma muy simple. Lo único que tenemos que hacer es guardar una matriz de casillas. Y por cada casilla, el gráfico que le corresponda. (además de la información que el juego necesite, por supuesto).
De momento. Podemos suponer que sólo tenemos que guardar el gráfico, así que podemos definir el mapa así:
int mapa[ANCHO_MAPA][ALTO_MAPA];
y si mapa[x][y] = 4, eso significa que en la posición (x, y) del mapa hay una casilla con el gráfico número 4 (guardamos simplemente un índice)
Claro, necesitaremos también los gráficos de cada casilla. En vez de crear una superficie para cada uno, como por regla general serán bastante pequeños, lo que hacemos es agrupar muchos en una única superficie. Y a eso es a lo que llamamos Tileset.
Un ejemplo con varios tipos de tiles:
http://www.rarefied.org/subspace/tileset.jpg
Así que lo que haremos para dibujar el mapa es recorrer la matriz, y por cada casilla, ver que “tile” hay que dibujar, y hacer un blit desde el “tileset” que contenga todos los tiles a la superficie destino (la pantalla).
De momento vamos a suponer que al Tileset solo hace falta indicarle el índice del tile que hay que dibujar, y la posición en la pantalla donde debe aparecer, y él se encarga de hacer el blit.
for (y = 0; y < ANCHO_MAPA; y++) {
for (x=0; x < ANCHO_MAPA; x++) {
dibujar mapa[x][y] en (posX, posY)
}
}
De momento aquí vemos algo curioso: Aparecen dos sistemas de coordenadas distintos
(x, y) son las coordenadas de la casilla en la matriz de casillas (el mapa)
(posX, posY) son las coordenadas en pixels del punto de la pantalla donde dibujaremos la casilla.
Coordenadas
Bueno, lo acabais de ver. Tenemos más de un sistema de coordenadas al convertir nuestra matriz de casillas en algo dibujado en pantalla. Lo que tenemos que ver es cuántos sistemas tenemos, y cómo pasar de uno a otro.
De momento, a (x, y) las vamos a llamar “Coordenadas lógicas” o “Coordenadas de mapa”
Y a (posX, posY) las llamaremos “World Coordinates”, o en español, “Coordenadas del Mundo”, o “Coordenadas Absolutas”
Al proceso de pasar de las coordenadas lógicas a las coordenadas absolutas lo vamos a llamar “Plotting”, o más específicamente: “Tile Plotting”
Al proceso de pasar de pasar de las coordenadas absolutas a las coordenadas lógicas lo vamos a llamar “Mouse Mapping” (lo del Mouse es porque se suele usar para detectar sobre qué casilla ha clickeado el jugador)
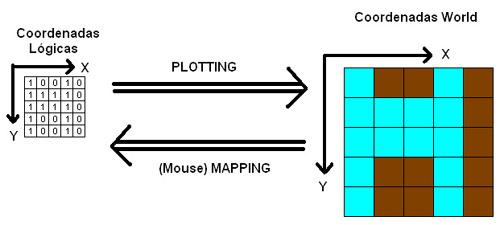
En nuestro caso pasar de un sistema de coordenadas a otro es muy sencillo. Suponed que cada tile tiene un ancho y alto de 50 pixels. Entonces:
- La casilla (0, 0) tiene las coordenadas absolutas (0, 0) (esquina superior izquierda)
- La casilla (1, 0) (la siguiente a la derecha) tiene las coordenadas absolutas (50, 0)
- La casilla (2, 0) (la siguiente) tiene las coordenadas abs. (100, 0)
- La casilla (2, 1), tiene las coordenadas abs. (100, 50)
- La casilla (x, y) tiene las coordenadas abs. (50 * x, 50 * y)
Así que:
plot (x, y) = (ANCHO_TILE * x, ALTO_TILE * y)
Y el proceso inverso es igual de sencillo:
mouseMap (x, y) = (x / ANCHO_TILE, y / ALTO_TILE)
Así que el algoritmo de antes se nos queda en esto:
for (y = 0; y < ANCHO_MAPA; y++)
for (x=0; x < ANCHO_MAPA; x++) {
tileset->dibuja (mapa[x][y], ANCHO_TILE * x, ALTO_TILE * y, pantalla);
}
(He supuesto que tileset tiene un método para dibujar los tiles que recibe el índice del tile, las coordenadas, y la superficie destino)
Desde luego, habrá que implementar ese método en tileset, que básicamente consistirá en averiguar qué rectángulo corresponde al tile indicado, y hacer un blit a las coordenadas que nos pasen, nada complicado.
Bueno, pues ya está. Aunque es un poco simple, no? Vamos a darle una vuelta de tuerca más:
Scrolling
Supongo que la mayoría sabréis en que consiste el scroll, pero bueno:
Imaginad que tenemos un mapa muy grande. Al ser tan grande, no cabe dentro de la pantalla, así que no podemos verlo todo de una vez. Lo que hacemos es que la pantalla se convierta en una “ventana” dentro del mundo del juego.
Y por supuesto, el jugador va a ir moviendo esa ventana, desplazándola de un lugar a otro:
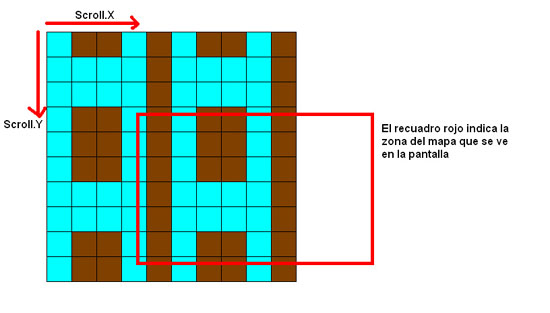
El desplazamiento de esa ventana es lo que llamamos “Scroll”, y lo mediremos siempre relativo a las coordenadas absolutas de la casilla (0,0). Así que este desplazamiento se medirá en pixels.
Con esto, introducimos un nuevo sistema de coordenadas. Además de lo que teníamos antes, ahora hay que tener en cuenta que las coordenadas de la casilla en la pantalla dependerán del desplazamiento de la pantalla respecto a la casilla (0,0).
Por ejemplo, la casilla con coordenadas lógicas (4, 1) puede tener las coordenadas absolutas (200, 50), y a la hora de dibujarse en pantalla, teniendo en cuenta el desplazamiento, puede que se dibuje en (451, 37).
A estas nuevas coordenadas las llamaremos “Coordenadas de Pantalla” (Screen Coordinates)
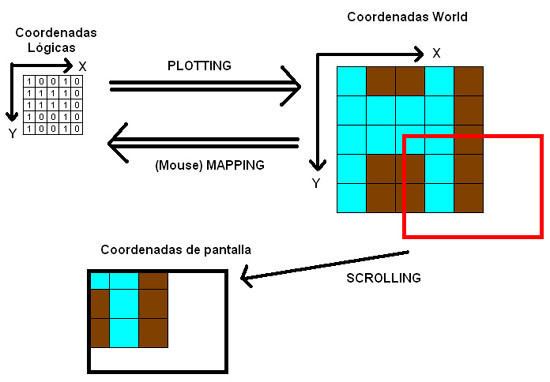
El convertir de coordenadas absolutas a coordenadas de pantalla es tan sencillo que lo podemos hacer como parte del plotting:
plot (x, y) = ((ANCHO_TILE * x) – scroll.x, (ALTO_TILE * y) – scroll.y)
Y al revés:
mouseMap (x, y) = ((x + scroll.x) / ANCHO_TILE, y / (y + scroll.y) ALTO_TILE)
Y por lo tanto el algoritmo se convierte en:
for (y = 0; y < ANCHO_MAPA; y++)
for (x=0; x < ANCHO_MAPA; x++) {
tileset->dibuja (mapa[x][y], (ANCHO_TILE * x) – scroll.x,
(ALTO_TILE * y) – scroll.y, pantalla);
}
Bueno, ya está, ahora sí.... Pero tampoco es mucho más complicado, ¿verdad? Sólo una resta...
Ya que hemos llegado hasta aquí, démosle otra vuelta de tuerca más...
Optimizaciones
Vale, volved a imaginar el mapa gigante. Es enorme. Ocupa el equivalente a 8 pantallas de ancho y 5 de alto. Son un montón de casillas. Pero sólo vamos a ver las que “quepan” en pantalla.
Entonces... ¿para qué estamos recorriendo todas las demás y diciéndoles que se dibujen? Si no se van a ver.
En programación gráfica, la primera regla de oro es “No dibujarás nada que no se vaya a ver en pantalla”, así que vamos a ver si podemos optimizar esto un poco, y evitar dibujar siempre todo el mapa.
Lo que está claro es que vamos a dibujar todas las casillas que estén dentro de la pantalla, es decir, estas:
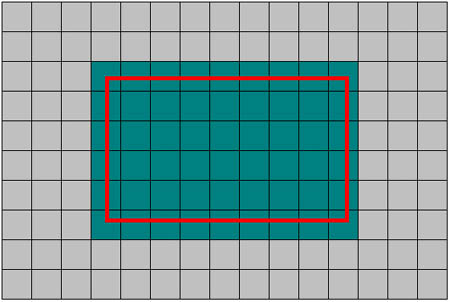
Todas las casillas marcadas en verde azuloide serán las que tengamos que dibujar. Todas las demás no hacen falta.
Asi que lo que tenemos que hacer es limitar el bucle de nuestro algoritmo a ese rectángulo verdi azuloide. Pero para hacer eso, necesitamos conocer cuáles son las casillas de sus esquinas. Necesitamos saber sus coordenadas lógicas, no?
No las tenemos, pero si que tenemos sus coordenadas de Pantalla. Si la pantalla es de 800x600, las coordenadas de pantalla de las esquinas son:
(0, 0) para la esquina superior izquierda
(800, 0) para la esquina superior derecha
(0, 600) para la esquina inferior izquierda
(800, 600) para la esquina inferior derecha
Si mapeamos estas coordenadas, obtendremos las coordenadas de las casillas que se encuentran en cada una de las esquinas. Es decir, las casillas que delimitan el rectángulo verdi azuloide. Es decir, las que debemos meter en nuestro bucle para dibujar sólo las que realmente son necesarias...
Pues venga:
inicial = mouseMap (0, 0);
limDerecho = mouseMap (800, 0);
limInferior = mouseMap (0, 600);
for (y = inicial.y; y < limInferior.y; y++)
for (x=inicial.x; x < limDerecho.x; x++) {
tileset->dibuja (mapa[x][y], (ANCHO_TILE * x) – scroll.x,
(ALTO_TILE * y) – scroll.y, pantalla);
}
NOTA: Sería necesario comprobar también si la casilla que vamos a dibujar es "válida". Es decir, está dentro del mapa, para no dibujar casillas como (-3, 0), por ejemplo.
Y ahora sí que sí, verdad?
No? Y que falta ahora?
Layering
¿Qué es el layering? Pues simplemente, tener varias capas de tiles por cada casilla. Si queremos guardar no sólo el tipo de terreno, sino también si hay un objeto en la casilla, necesitamos más información que un simple entero.
Lo que tenemos entonces son varios “tiles” en una casilla, que se dibujan desde el fondo hacia arriba (primero el suelo, luego los objetos, etc...).
En nuestro caso lo que haremos será que la casilla no sea un “int”, sino una estructura (o clase) Casilla, que guardará el tipo de suelo, pero también el tipo de pared, si tiene algún objeto, etc...
A la hora de dibujarlo, habrá que dibujar todo eso en orden:
tilesetSuelos->dibuja (mapa[x][y].tipoSuelo, (ANCHO_TILE * x) – scroll.x,
(ALTO_TILE * y) – scroll.y, pantalla);
tilesetParedes->dibuja (mapa[x][y].tipoPared, (ANCHO_TILE * x) – scroll.x,
(ALTO_TILE * y) – scroll.y, pantalla);
tilesetObjetos->dibuja (mapa[x][y].tipoObjeto, (ANCHO_TILE * x) – scroll.x,
(ALTO_TILE * y) – scroll.y, pantalla);
Y os podeis imaginar que será algo más complicadillo, ¿verdad?
Bueno, pues ahora si que he terminado. Un saludo xD
|